平成25年度春期 プロジェクトマネージャ試験 午前II 問8
【問題8】
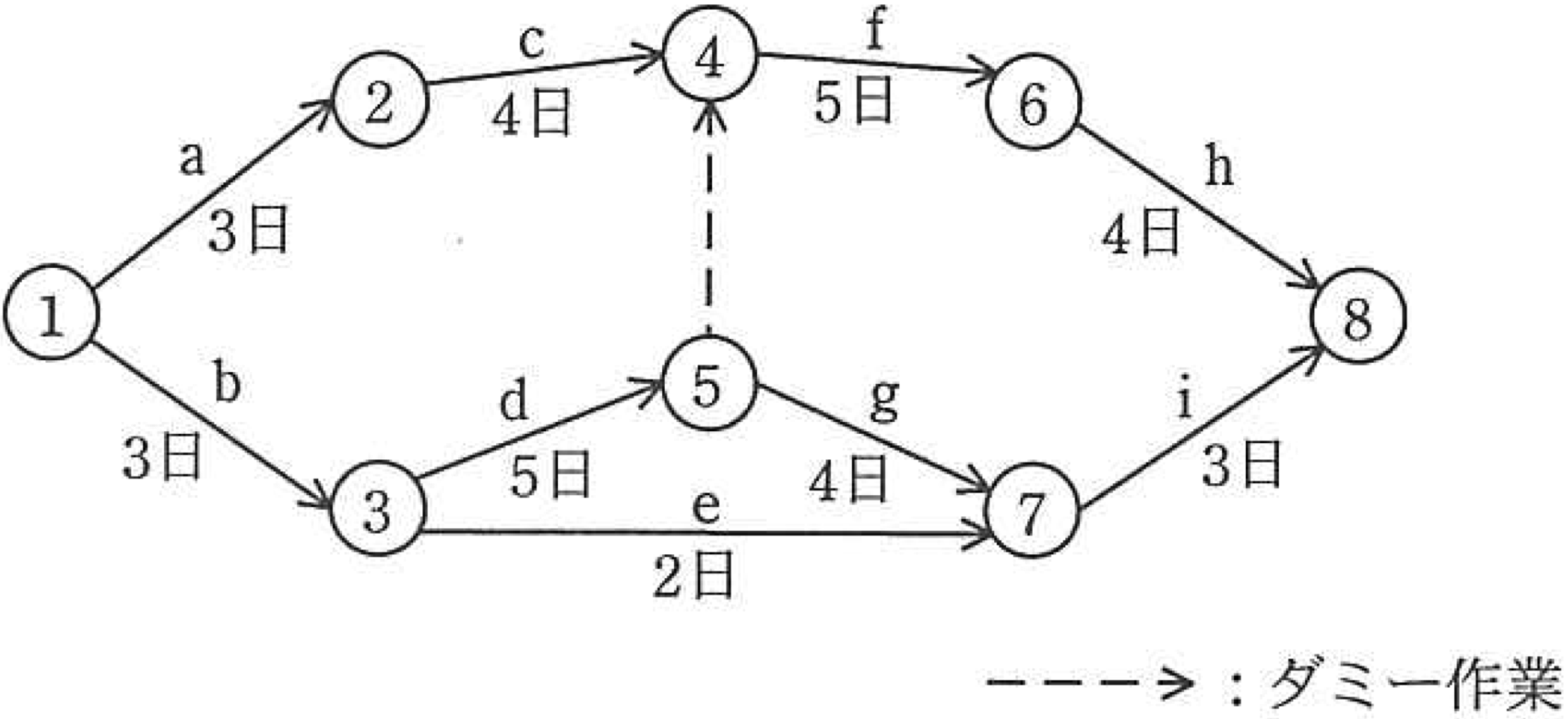
次のアローダイアグラムを基にして要員計画を立てる。要員数の増減を極力抑え、かつ、最短日数で終えられるように計画を立てる場合、1日当たりの最大要員数は何名になるか。ここで、各工程は1名で作業するものとする。
【解説】
1. 各経路の所要日数を計算
アローダイアグラムに基づいて、各経路の所要日数を計算します。
- 経路 a → c → f → h(1 → 2 → 4 → 6 → 8)
所要日数 = 3日(a) + 4日(c) + 5日(f) + 4日(h) = 16日
- 経路 b → d → f → h(1 → 3 → 5 → 6 → 8)
所要日数 = 3日(b) + 5日(d) + 5日(f) + 4日(h) = 17日
- 経路 b → d → g → i(1 → 3 → 5 → 7 → 8)
所要日数 = 3日(b) + 5日(d) + 4日(g) + 3日(i) = 15日
- 経路 b → e → i(1 → 3 → 7 → 8)
所要日数 = 3日(b) + 2日(e) + 3日(i) = 8日
クリティカルパスは、所要日数が最も長い経路であるため、経路 b → d → f → h(17日) です。
2. 同時進行する作業を確認
クリティカルパス上および他の経路の作業を考慮して、同時に進行する作業を確認します。
- 1日目~3日目
作業 a(1 → 2)と作業 b(1 → 3)が同時進行。要員数 = 2名。
- 4日目~7日目
作業 c(2 → 4)と作業 d(3 → 5)が同時進行。要員数 = 2名。
- 8日目
作業 d(3 → 5)が進行。要員数 = 1名。
- 9日目~12日目
作業 f(4 → 6)と作業 g(5 → 7)が同時進行。要員数 = 2名。
- 13日目
作業 f(4 → 6)と作業 e(3 → 7)が同時進行。要員数 = 2名。
- 14日目
作業 h(6 → 8)と作業 e(3 → 7)が同時進行。要員数 = 2名。
- 15日目~17日目
作業 h(6 → 8)と作業 i(7 → 8)が同時進行。要員数 = 2名。
3. 最大要員数
最も要員数が多いのは、 2名 です。
出典:平成25年度 春期 プロジェクトマネージャ試験 午前II 問8
![]()